＜「これだけ知っていればなんとかなる」計画化の理論とツール ②：主要な戦略の型＞

マネジメント実践者によるマネジメント実践者のための
『これだけ知っていればなんとかなる』マネジメント探究の考房

＜「これだけ知っていればなんとかなる」計画化の理論とツール　②：主要な戦略の型＞

　「戦略の型」は、どうやって成長するか（成長戦略）、どうやって競争に勝つか（競争戦略）、どうやって逃げるか（撤退戦略）の３つに大別できます。それぞれについて主要な理論を紹介します。

■成長戦略

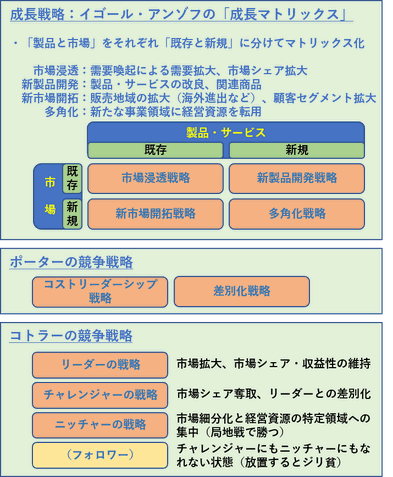
　イゴール・アンゾフの「成長マトリックス」は「製品（あるいはサービス）と市場」をそれぞれ「既存と新規」に分けて２×２のマトリックス化して、４つの戦略の型を示しています（右図）。多角化は事業リスクの分散、範囲の経済の実現、遊休経営資源の活用にメリットがありますが、未踏の領域への進出なので失敗のリスクも大きくなります。

■競争戦略

　マイケル・ポーターは競争戦略の型として、①コストリーダーシップ戦略②差別化戦略という２つの型を提示しています（元々はこれらに加えて集中戦略がありましたが、近年では「無視してよいだろう」がコンセンサスになっています）。

　コストリーダーシップはあくまでもコストの優位であって、必ずしも価格引き下げを意味するものではありません。コスト優位の源泉として、規模の経済（スケールメリット）、学習・習熟によるコスト低減、技術によるコスト低減があります。

　差別化は製品（あるいはサービス）の素材・機能・品質・品揃え・ブランド力、顧客対応、タイミング、ロケーションなどの優位を源泉とします。

　「マーケティングの神様」フィリップ・コトラーは有効な戦略は市場でのポジション（地位）によって違うと主張し、市場での４つのポジション（地位）とそれぞれの戦略の型を提示しています。

　「ニッチャー」は「ニッチを志向する者」という意味で、ニッチ（niche）は隙間、ビジネスにおいては大企業が狙わないような領域を指します。

　コトラーの４つのポジションに対して、「強者と弱者」という風に２つに分けたのがランチェスター戦略と呼ばれるものです。主にマーケティング戦略として扱われることが多いようですが、事業戦略としても含意が大きいと思います。

　中小企業が大企業と相対する際には「弱者の戦略」が有効ですし、大企業同士の戦いであっても正面きって仕掛けるのでなく、局地戦の展開をつくって、そこでは数の優位で相手をせん滅するといったことも消耗を避けて効率的に勝つには有効な作戦です。ゲリラ戦法は大きな軍隊でも個別の戦闘において活用できますし、強者は相手にゲリラ戦に持ち込ませないのが大事ということも言えます。

■撤退戦略

　ビジネスはうまうゆくことばかりではなく、むしろ失敗することの方が多いかもしれませんので「どうやって逃げるか」は常に考えておく必要があります。

　撤退の戦略は、損失を極小に抑えながら（あるいは利益を確保しながら）徐々に撤退する収穫戦略と経営資源を転用もしくは売却（あるいは損失を一気に清算）することでできる限り早く撤退する即時撤退戦略に大別されます。

　手遅れにならないタイミングを見極め、事業再生の可能性・現実性、撤退の影響と対応を熟慮することが必要です。

■PPM（プロダクト・ポートフォリオ・マネジメント）

　PPMは経営戦略系の参考書には必ず出てくる有名な理論なので紹介しておきます。

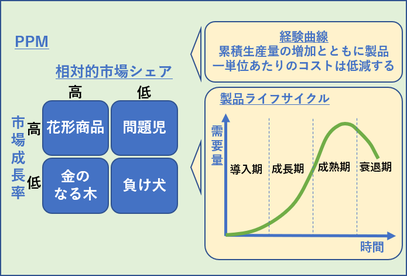
　ボストン・コンサルティング・グループが開発した事業（商品）ミックス戦略のフレームワークで、市場成長率の高低と相対的市場シェアの高低をマトリックス化して2×2のマスに4種の事業特性を表したものです。

　相対的市場シェアは販売ボリュームと同時に収益性を表すものと想定されています。これは、累積生産量の増加とともに製品一単位あたりのコストが低減するという経験曲線を前提としています。PPMのもう1つの前提は「製品には誕生から消滅までの寿命がある」という考え方（プロダクト・ライフサイクル：PLC）です。

　きれいなフレームワークなのでウンチクとして知っておくのはよいと思いますが、実用の用途はあまりなさそう・・・です。PPMを改良したものとしてビジネス・スクリーン（BS）というものもありますが、これは「自社の事業強度」と「市場の魅力度」を3×3のマトリックス化したものです。

＜補論1＞　ランチェスター法則：簡単な計算をしてみる

　ランチェスター戦略の元になってるランチェスター法則はイギリス人エンジニアのF.W.ランチェスター（1986～1946年）が生み出したものと言われています。ランチェスターは2つの法則を提示しました。実際に簡単な計算をしてみましょう。

第一法則：一騎討ちの法則

　ひとりがひとりしか狙い撃ちできない「一騎討ち型の戦闘」（＝槍とかピストル）においては、戦闘後の残存兵力数は両軍の兵器の性能と初期の兵数によって決まる

　M0－M＝E（N0ーN）

　（例）味方が５人、敵が３人で兵器の能力が同等であれば、敵が全滅したときに味方は２名残存（＝3名損失）する

　　　　計算式：　5－M＝3－0　⇒　M＝2

　M0は味方の初期兵数、Mは戦闘後の味方の残存兵数、N0は敵の初期兵数、 Nは戦闘後の敵の残存兵数、 Eは兵器の性能の比

第二法則：確率戦闘の法則

　機関銃や航空機による爆撃のような確率兵器を使用する戦闘の場合、敵と味方の双方の攻撃力の比は兵数の二乗となり、初期兵数、戦闘後の残存兵力数、武器の性能の関係は以下のようになる

　M02－M2＝E（N02ーN2）

　（例）味方が５人、敵が３人で兵器の能力が同等であれば、敵が全滅したときに味方は4名残存（＝1名損失）する

　　　　計算式：　52ーM2＝32－０2　⇒　 M2＝16　⇒　M＝4

　ポイントは、兵器の性能が同等であれば、①兵数の多い方（＝強者）が勝つ、②確率兵器は兵数の多い方（＝強者）に極めて有利に働くということです（上の例では、初期兵数が味方5人で敵3人の場合、敵を殲滅した後の味方の損失兵数は一騎討ちの場合は3名に対して確率戦闘ではわずかに1名で済む）。

　では、ランチェスター法則に基づいて、「弱者が強者に勝つ」にはどうしたらいいのか？

　敵の初期兵数が9人、味方の初期兵数が6人の場合（つまり、敵が強者で味方が弱者）、もし、確率戦闘で正面から戦いを挑めば、結果は以下のようになります。

　　92－M2＝62－02　⇒　 M2＝ 92－ 62 　⇒　 M2＝45　⇒　M＝6.71

味方が全滅し、敵は6.71人残る（＝2.29人を失う）ということです。

　では、敵の兵力を3つに分散させて1つ1つを順番に叩くことができたらどうなるか？

　第一戦闘（今度は味方が6人で敵が3人なので、味方が強者です）

　　62－M2＝32－02　⇒　 M2＝ 62－ 32 　⇒　 M2＝27　⇒　M＝5.20

　第二戦闘（味方が5.20人で敵が3人なので、味方が強者です）

　　5.202－M2＝32－02　⇒　 M2＝ 5.202－ 32 　⇒　 M2＝18　⇒　M＝4.24

　第三戦闘（味方が4.24人で敵が3人なので、味方が強者です）

　　4.242－M2＝32－02　⇒　 M2＝ 4.242－ 32 　⇒　 M2＝9　⇒　M＝3

結果は、敵を殲滅した後に味方は３人が残り、見事に「弱者が強者に勝つ」を達成ということになります。

　ただし、上記の試算は「弱者の戦略」として「局地戦」の有効性を示すものですが、「一騎討ち」そのものの有効性を示すものではありません。もし、弱者が局地戦で一騎討ちを実行すれば、最後には弱者は全滅し、兵数に勝る強者が3名残る（９－6＝3）ことになるのです。実際には、弱者が強者に比べて局地戦において何かしらのアドバンテージを持っていること（例えば地場企業が大企業に比べて地域の市場特性をより深く理解しているなど）もあるでしょうし、弱者が強者の確率戦闘を封じるような戦闘環境を作ることは、仮に強者が勝っても甚大な被害を被る（上の例では9人のうち6人を失う）ことから戦闘そのものを抑止させる防衛的な効果を狙うことに意味があると考えるべきでしょう。